Interpretablity of Language Models Using Category Theory

Context

During my undergrad at McGill in Fall of 2022, I did an honours independent study (MATH480) with Professor Prakash Panangaden. It all started when, inspired by this blog post & paper, I emailed Prakash asking for his supervision to study applied category theory. He responded, “Oh no! Another person fallen victim to the siren song of category theory. Well, when you put it like that how can I say no?” and the rest was history.

What did I study?

Basic concepts of category theory from Prakash’s notes and other diverse sources
What is applied category theory by Tai-Danae Bradley
Selected chapters from Seven Sketches in Compositionality: An Invitation to Applied Category Theory by Brendan Fong and David Spivak

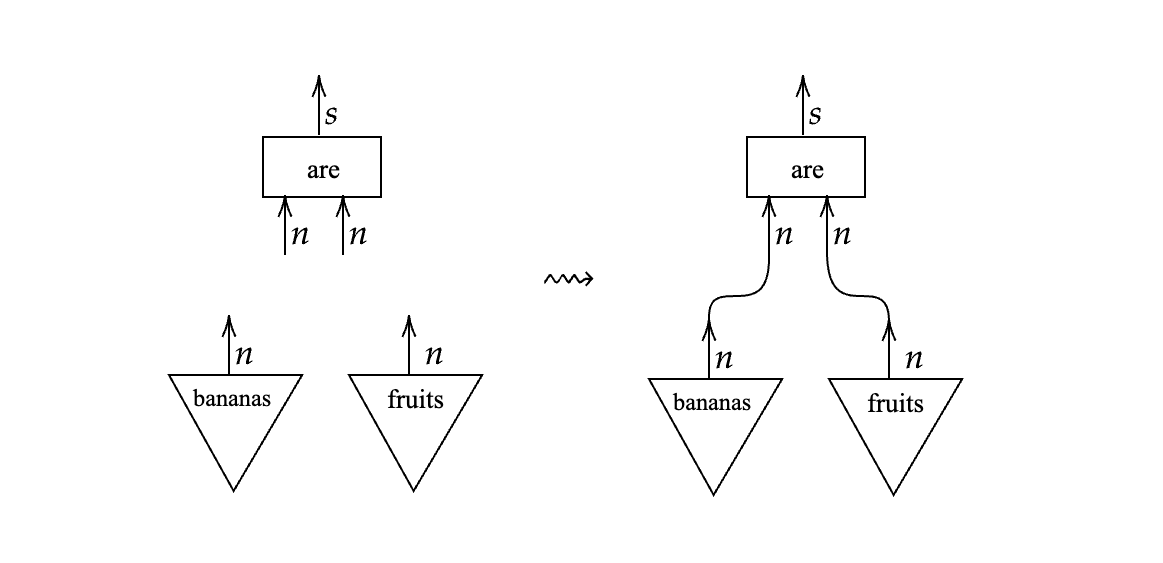
My goal was to learn enough category theory to deeply understand An enriched category theory of language: from syntax to semantics by Tai-Danae Bradley, John Terilla, and Yiannis Vlassopoulos. I am proud to say I achieved this goal and wrote a term paper with a discussion on the feasibility, applications, and future implications of using category theory for interpretable NLP on a broader scale.

One of my favourite parts was getting into the syntax category and representing it with string diagrams!

Reflections

I thoroughly enjoyed the abstractness of it all, feeling really inspired by just how lost I felt in the difficulty of the math but deeply satisfied each time I realized just how simple and intuitive each concept was (behind seemingly endless complex notation…). Especially when those concepts could be brought back down to a wide array of applications in math and beyond! Moreover, I was deeply humbled and learned when and how to ask questions and properly grapple with intense and difficult mathematical concepts both by myself, with a friend (Tasmin Chu), and with the help an incredible mentor like Prakash. In this semester, I learned a lot about myself and how I like to learn (via teaching!) because for the first time, I pursued a topic out of sheer curiosity that I knew I would never need or use ever again. I also became very proficient in making LaTeX TikZ diagrams (my favourite editor is mathcha.io).

Basically, in this semester I came to the conclusion that the abstractness of math is indeed cool/beautiful, but for me to personally really enjoy it, I needed (a) to be able to visualize it and (b) to grasp concrete examples or applications of everything. I also knew by this point I didn’t want to pursue a PhD in mathematics, though this would have been a cool path if I’d chosen to do so…

A screenshot of my notes on the yanking equations, something that looks and feels really complicated until you draw it out! String diagrams save the day!